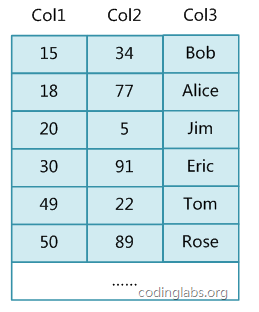
数据库索引是提高数据库性能的一个十分重要的工具,数据库索引究其根本是一种数据结构,目前大部分数据库的索引都是以B+树来实现的,当然也有部分是通过哈希表。之前在使用索引的时候,只知道索引好比一本书的目录一样,可以提高数据查询的性能,但是对其实现原理并不是很了解,所以这里深入了解一下B/B+树以及数据库索引的实现原理。
B树
B树的定义
B树简单来说就是一棵多叉的平衡查找树,m(m>=2)阶B树的定义如下:
- 树中的每个节点最多有m个孩子。
- 除了根节点和叶子节点之外,其他节点至少有m/2(向上取整)个孩子。
- 根节点至少有2个孩子(除非根节点是叶子节点)
- 每个节点有n个关键字,并按升序排列。含有n个关键字的节点有n+1个孩子。所以n要满足
\(\frac{m}{2}-1\leq n\leq m-1\) - 所有的叶节点都在同一层。
下图是一棵3阶B树的建树过程。依次插入6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4

B树的高度
B树的高度
\[h\leq\log_t\frac{n+1}{2}\]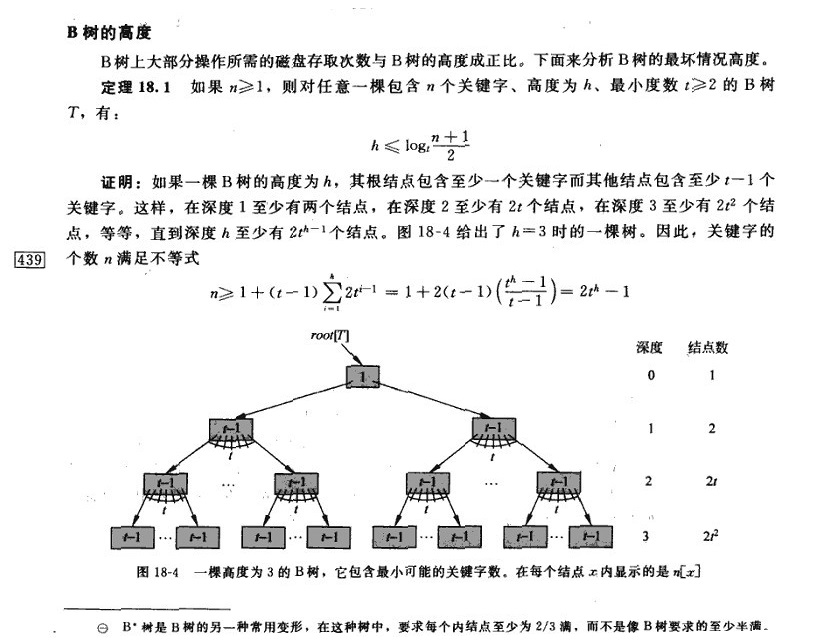
这里的t其实相当于是m/2,因为每个节点至少有m/2个孩子。
所以B树的搜索复杂度为\(O(\log_tN)\)
B+树
B+树是在B树基础上的一个改进,其基本定义与B树相同,差异在于:
- 含有n个关键字的节点有n个孩子。
- 非叶节点仅具有索引作用,跟记录有关的信息均存放在叶节点中。(也就是说,非叶节点中是没有指向数据记录的指针的,指向数据记录的指针只存在于叶节点中)
- 树的所有叶节点构成一个有序链表,可以按照关键字的顺序遍历全部记录。
下图是一棵3阶B+树的建树过程

从建树的过程来看,主要区别在于分裂的时候,并不是直接将一个元素拉到上一层中,而是“复制”(这里说复制其实不准确,因为没有复制数据信息,只是有关键字的信息)一份放到上一层,同时本节点分裂,这样也就保证了在叶节点中是存了所有的数据(记录)的。
为什么使用B/B+Tree作为索引实现?
为什么使用B/B+Tree来作为索引的实现,而不用二叉平衡树或者红黑树呢?这与计算机的组成原理,特别是磁盘IO有着很大的联系。
一般来说,索引本身也是比较大的(毕竟也是一棵树啊),不可能全部存储在内存中,而是以索引文件的形式存储在磁盘上。这样,在使用索引的时候就会产生I/O消耗。所以,尽量减少I/O操作次数是一个好的索引结构应该考虑的很重要的事情。所以,这就要涉及到计算机硬盘的一些操作原理。
磁盘存取原理
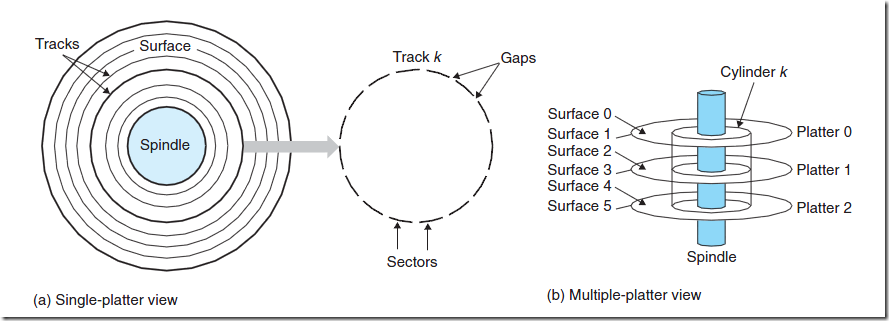
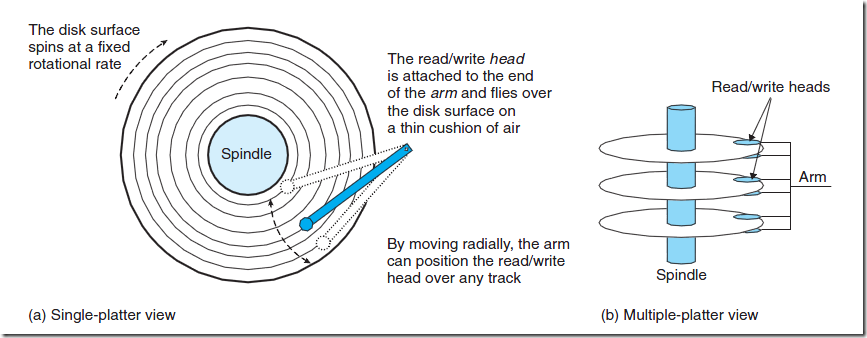
如图所示,一个磁盘由大小相同且同轴的多个圆形盘片组成,它们可以同步转动。每一个盘片有正反两个盘面(surface),盘片中央有一个可旋转的主轴(Spindle)。每一个盘面被划分为多个同心圆,成为磁道(Tracks),多个盘面上下重合的磁道组成了一个柱面(Cylinder)。每一个磁道又被划分为多个扇区(Sectors),中间由一些间隔(gap)分开。每个扇区是硬盘的最小存储单元,通常为512字节。
当需要读取数据时,系统会将数据逻辑地址传给磁盘,磁盘的控制电路按照寻址逻辑将逻辑地址翻译成物理地址,即确定要读的数据在哪个磁道,哪个扇区。为了读取这个扇区的数据,需要将磁头放到这个扇区上方,为了实现这一点,磁头需要移动对准相应磁道,这个过程叫做寻道,所耗费时间叫做寻道时间,然后磁盘旋转将目标扇区旋转到磁头下,这个过程耗费的时间叫做旋转时间。
局部性原理和磁盘预读
由于磁盘本身的读取比内存要慢很多,为了减少磁盘I/O,磁盘通常不是严格按需读取,而是每次会按顺序向后预读一定长度的数据放入内存,这样做是依据计算机科学中著名的局部性原理:
当一个数据被用到时,其附近的数据也通常会马上被使用
程序运行期间所需要的数据通常比较集中
由于顺序读取的效率很高(只需要旋转时间,而不需要寻道时间),因此,因此对于具有局部性的程序来说,预读可以提高I/O效率。
预读的长度一般为页(page)的整倍数。页是计算机管理存储器的逻辑块,硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块,每个存储块称为一页(在许多操作系统中,页得大小通常为4k),主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时,会触发一个缺页异常,此时系统会向磁盘发出读盘信号,磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中,然后异常返回,程序继续运行。
B/B+Tree索引的性能分析
在了解了以上硬盘的存取原理后,就可以来分析到底为什么使用B/B+Tree来作为索引实现了。
数据库系统的设计者巧妙地利用了磁盘预读的原理,将一个节点的大小设为等于一个页(每次新建节点时,直接申请一个页的空间,这样就保证了一个节点在物理上是存储在一个页中的),这样,每个节点只需要一次I/O就可以完全载入。
对于B树来说,检索一次最多需要访问的节点数目是树高-1(根节点通常常驻内存),而树高\(h\leq\log_t\frac{n+1}{2}\),这里的t通常是比较大的,这样,一次查询操作只需要h-1次I/O操作,所以效率非常高。
而B+树比B树更适合做索引的原因在于,B+树的非叶节点中是不包含数据的,因此一个节点所能存储的关键字数据就会更多,也就是t就更大,这样性能就会更好。
小tips:t的大小是由页的大小、关键字大小以及指针大小共同决定的,页的大小通常固定,所以t的大小主要看关键字,如果关键字很大,那么t也有可能很小,因此,最好不要在大的关键字上建立索引哦。
使用B+树的一个另一个原因是,B+树的叶节点是按顺序连接在一起的,这样就可以快速遍历整个数据,这样在做一些基于范围的查询时速度会很快,而B树这种操作的效率会很低。
而对于红黑树或者二叉树这种结构,树要深很多,而且逻辑上很近的父子节点在物理上可能会差很远,I/O消耗可能就非常大了。
复合索引
之前我们讨论的都是在单个关键字上建立索引,那么对于复合索引,其原理是一样的,同样也是一棵B+树。
在建立索引的时候,会按照关键字的先后顺序,先比较第一个,第一个相同再比较第二个,以此类推。这也就是为什么在建立了复合索引后,只有匹配最左前缀才能用到索引。
Mysql的索引实现
Mysql中,索引是存储引擎级别的概念,不同的引擎对索引的实现方式是不同的,这里选取了两个典型的结构来探讨一下
InnoDB索引实现
InnoDB应该是Mysql里使用最多的存储引擎了,它的索引实现是使用的B+Tree。这里假设我们的数据表结构如下:
InnoDB索引的一个重要特点是,其数据文件本身就是一个索引文件。这个索引就是该数据表的主键,这种索引也叫做聚集索引。
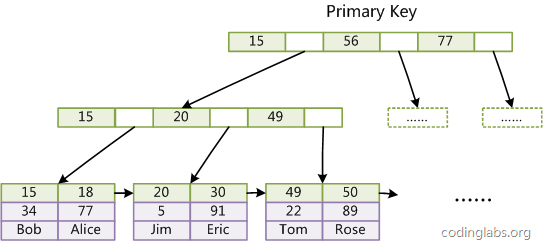
可以看到,InnoDB的叶节点中的数据域保存了完整的数据记录。因为InnoDB的数据文件本身要按主键聚集,所以InnoDB要求表必须有主键。如果没有显式指定,则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键,如果不存在这种列,则MySQL自动为InnoDB表生成一个隐含字段作为主键,这个字段长度为6个字节,类型为长整形。
在InnoDB上建立辅助索引时,叶节点的data域保存的是相应记录的主键值。
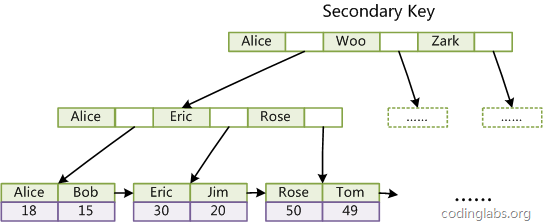
聚集索引的实现方式使得按主键进行检索十分高效,但是辅助索引就要检索两遍了:首先检索辅助索引获得主键,然后利用主键检索获取记录。
在知道了InnoDB的索引实现原理之后,就会对我们使用索引有一定的指导作用了。例如:不建议用过长的字段作为主键,因为所有的辅助索引都会引用主键,这样会让辅助索引变得很大。再例如:用非单调的地段作为主键在InnoDB中不是个好主意,因为非单调的主键在插入新纪录的时候会为了维持B+Tree的平衡而进行很多平衡操作,所以,建议用自增字段作为索引。
MyISAM索引实现
这个引擎没有用过,但是他的索引实现和InnoDB完全不同,所以这里拿出来分析一下。
MyISAM引擎同样适用B+树作为索引实现。下面是其原理图:
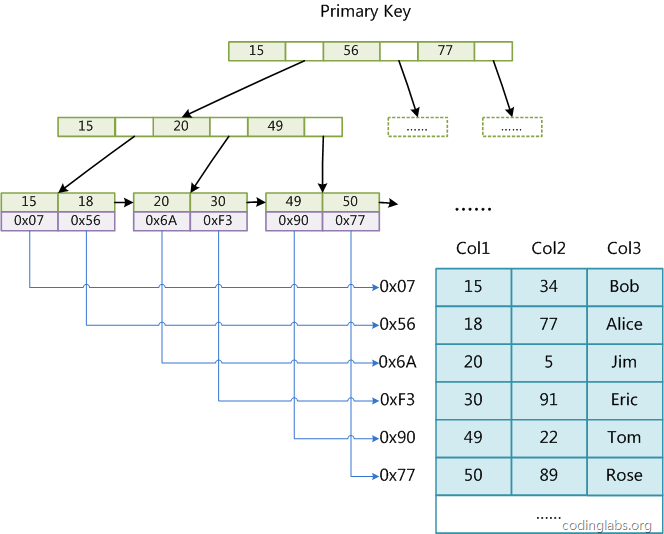
从图中可以看到,MyISAM的索引文件只保存了数据的地址。而辅助索引和主索引没有区别,只是主索引要求key是唯一的,而辅助索引的key可以重复。
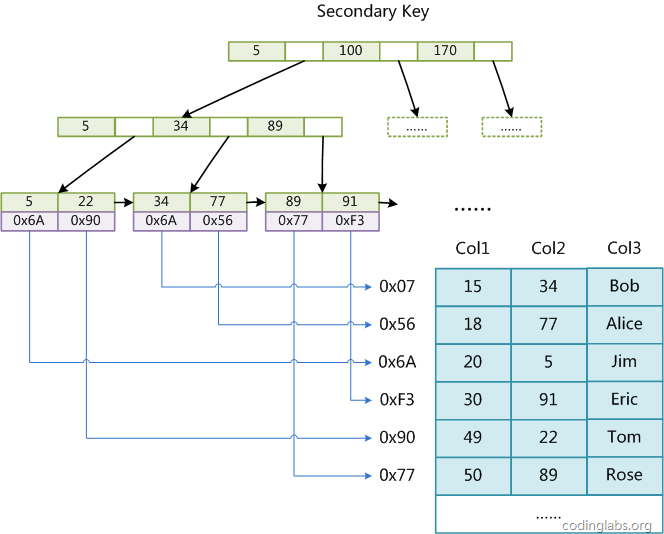
所以,MyISAM索引检索时先按照B+Tree搜索索引,获取到data域中存的地址后,读取相应的数据记录。
MyISAM的这种索引方式也叫非聚集索引。
MongoDB的索引实现
Mongodb的索引也是以B-Tree的形式实现的(但是不知道是B还是B+)。至于是聚集索引还是非聚集索引,没有找到更多的资料。实验了一下,在一个mongo数据库中新建一个collection然后插入一条文档,在对应的数据库文件夹下多了一个collection文件,同时多了一个index文件,所以我猜mongo的实现是非聚集式的。
哈希索引
除了B-Tree或者B+Tree,有的索引是采用哈希表来实现的。简单来说,就是将关键字作一次哈希计算,然后根据哈希值来查找数据。所以哈希索引和树形索引的区别就显而易见了:
- 对于等值查询,哈希索引是有明显优势的,只需要一次哈希计算就可以了。当然,这要在哈希碰撞发生的比较少的情况下,如果有大量重复的键值存在,哈希索引的等值查询效率也不见得很高。
- 对于范围查询,哈希索引就无能为力了,他不能像树那样一层层向下查找。同样,哈希索引也不能用于排序。
- 哈希索引也不能支持左缀匹配,因为计算哈希值必须要完整的关键字。