红黑树是一种特殊的二叉查找树，它在二叉查找树的基础上，在每个节点增加了一个表示颜色（红和黑）的量，使得其可以基本保持平衡，但又不需要像平衡二叉查找树那样在平衡操作上花费很多时间。STL以及Linux内核中平衡树的实现采用的都是红黑树，所以，了解红黑树的基本原理还是很重要的。
（题图Photoed by Luis Llerena）
前置知识
二叉查找树
二叉查找树（Binary Search Tree, BST）是一种特殊的二叉树，它保证任意节点的左子树的值均小于它的根节点的值，而右子树的值大于根节点的值。理想情况下，BST的树高是\(\log N\)，因此其查找和插入的复杂度基本为\(O(\log N)\)，而删除节点的操作需要将被删除节点与其左子树中的最大值或者右子树中的最小值互换，这一过程的复杂度也不会超过\(O(\log N)\)。
但是，在极端情况下，即建树的过程中，数据是按大小顺序排列好的，BST就会退化为一个单向链表，其查找和插入的平均复杂度在\(O(N)\)数量级上。
二叉平衡查找树
二叉查找树在树两端极度不平衡的情况下，性能会变得比较差，所以二叉平衡查找树（AVL Tree）就诞生了。AVL 树通过旋转操作，保证了在建树的过程中树的左右子树高度相差不超过1（平衡因子不超过1）。
因此，AVL树的查找复杂度为\(O(\log N)\)，插入的时候也只需要在不平衡的时候做一次单旋或者双旋操作，所以插入的复杂度也在\(O(\log N)\)数量级。而删除节点需要检查从被删除的节点到根节点路径上所有节点的平衡因子，需要的旋转操作的次数最多可能有\(\log N\)次，所以删除的代价稍微大一些，大约为\(O(2\log N)\)。
红黑树
性质
首先需要知道的是，红黑树是一棵二叉查找树，在此基础上，红黑树拥有以下5个性质：
- 节点是红色或者黑色
- 根是黑色
- 所有叶子节点都是黑色（叶子节点是NIL节点）
- 每个红色节点的子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点
这5条性质保证了有N个节点的红黑树高度为\(2\log (N+1)\)，从而保证其查询、插入、删除的复杂度不会过高。但同时又保证了一定的平衡性。
注：这里的高度可能不是很准确，但误差不会很大，可以查看相关文献，有更加准确的证明过程。
插入操作
红黑树的插入操作同样需要旋转操作来对树进行平衡，同时还需要一些着色操作。总结来说有三点：
- 插入的节点都是红色的（这样可以保证不破坏性质5，当然，如果插入的是根节点，直接涂黑就好了）
- 当插入节点的父节点是黑色时，红黑树的性质能够保持，不用变化
- 当插入节点的父节点是红色时，需要进行旋转或者重新着色来维持红黑树的性质。
所以，下面重点来看当插入节点的父节点是红色时，如何来进行旋转和着色。
这种情况下会有三种子情况，下面分别讨论。
-
插入节点的父节点和其叔父节点都为红色时
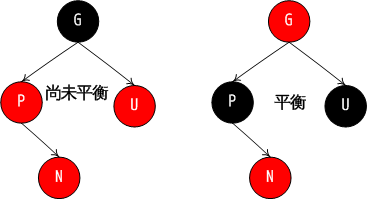
这种情况下，只需要将父节点和叔叔节点涂黑，将祖父节点涂红。这样可能会造成祖父节点不满足红黑树的性质，这时可以将祖父节点当作新插入的节点，再按照三种情况进行调整。
-
叔叔节点为黑色或者为空，且祖父节点、父节点和插入节点不在同一条斜线上。
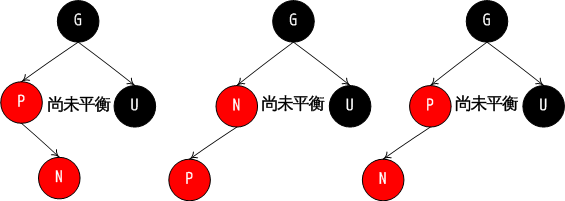
这种情况下，先将父节点进行左旋，使得祖父节点、父节点和插入节点在同一条斜线上，然后就可以按照下一种情况调整
-
叔叔节点为黑色或者为空，且祖父节点、父节点和插入节点在同一条斜线上。
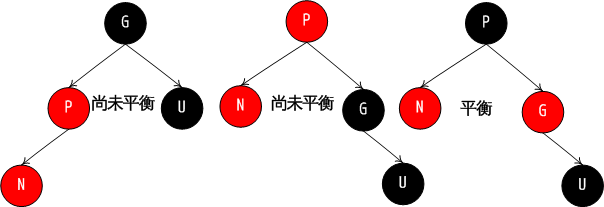
这种情况下先将父节点（P）涂成黑色，祖父节点涂成红色，然后将父节点P右旋。
以上就是红黑树的所有插入调整的情况。当然这里只是按照图片来讲解的，至于是左旋还是右旋，根据插入节点的位置类比得到。
下面是在一棵红黑树上插入节点的调整过程示例:
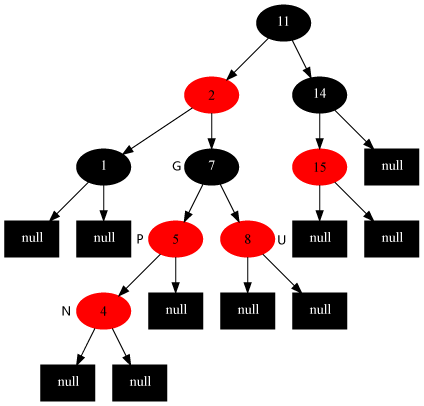
如图所示，我们在红黑树中插入节点N，这时N的父节点和叔父节点都是红色，所以按照情况1来调整,变成如下图所示的情况
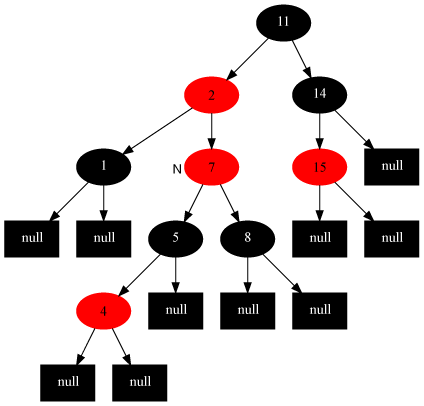
祖父节点不满足性质要求，所以继续以祖父节点为插入节点来进行调整，可以看到是情况2，调整后如下图所示：
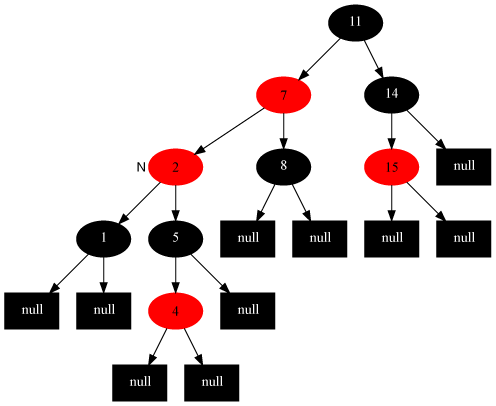
这时的红黑树又变为了情况3，所以再次调整，可以得到最终的红黑树：
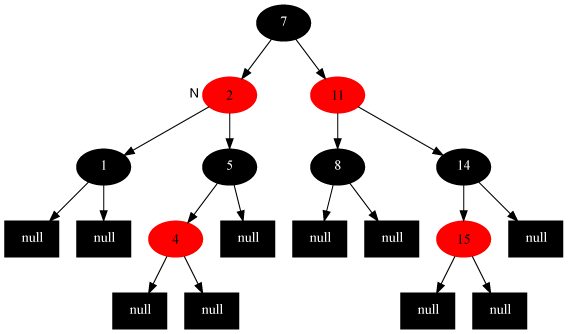
删除操作
红黑树的删除操作比插入操作要复杂一些，但是总体还是可以分为几种情况来讨论。
首先，红黑树的删除操作同样要先进行二叉搜索树的删除操作：
- 如果待删除节点没有子节点，那么直接删掉就可以了。
- 如果待删除节点只有一个子节点，删除掉该节点，并用其子节点去顶替。
- 如果待删除子节点有两个子节点，那么就找到左子树中的最大值或者右子树中的最小值（后面统称为交换节点），与待删除节点交换。而被交换的节点必然最多只有一个子节点，所以就转换为前两种情况。
而红黑树删除操作的关键在于，节点删除之后，如何来维持红黑树的性质。如果被删除的是一个红色节点，那么红黑树的性质是不会被破坏的，所以，下面主要考虑，被删除的节点是黑色节点的情况。
重要提示：这里指的“被删除节点”指的是实际被删除的那个，也就是说，是交换过后的那个节点，那个原本存的“左子树中的最大值或者右子树中的最小值”，而现在存的是要删除的值的那个节点。该节点最多只可能有一个非NIL的子节点，这个子节点会顶替被删除节点的位置。下文中，我们用“当前节点”来指代这个子节点。如果被删除节点没有非NIL子节点，那么当前节点就是一个NIL节点。
如果当前节点是黑色的根节点，那么不用进行任何操作。
如果当前节点是红色的，那么只需要把当前节点涂黑就可以了。
当遇到以下四种情况时，就需要进行一些旋转着色操作了：
- 当前节点是黑色的，且兄弟节点是红色的（那么父节点和兄弟节点的子节点肯定是黑色的）
- 当前节点是黑色的，且兄弟节点是黑色的，且兄弟节点的两个子节点均为黑色的
- 当前节点是黑色的，且兄弟节点是黑色的，且兄弟节点的左子节点是红色，右子节点时黑色的
- 当前节点是黑色的，且兄弟节点是黑色的，且兄弟节点的右子节点是红色，左子节点任意颜色。
可以看到，2、3、4其实是“当前节点是黑色的，且兄弟节点是黑色的”的三种子集。这里我们假设当前节点是父节点的左节点，右节点的情况可以镜像得到。
情况1：当前节点是黑色的，且兄弟节点是红色的
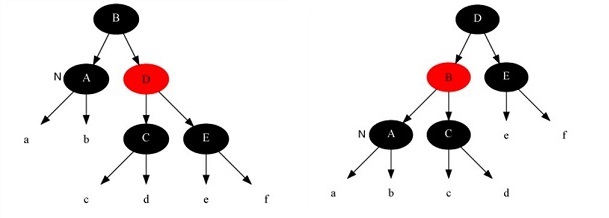
A节点表示当前节点。针对这种情况，我们要做的操作有：将父节点（B）涂红，将兄弟节点（D）涂黑，然后将当前节点（A）的父节点（B）作为支点左旋，然后当前节点的兄弟节点就变成黑色了，这样就就转换成情况2、3、4的特征了。
情况2：当前节点是黑色的，兄弟节点是黑色的，且兄弟节点的子节点都是黑色的
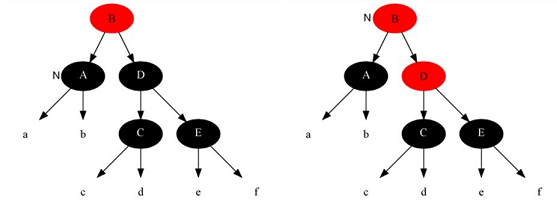
针对这种情况，我们要做的操作有：将兄弟节点（D）涂红，将当前节点指向其父节点（B），将其父节点指向当前节点的祖父节点，继续新的算法（具体见下面的程序），不需要旋转。
情况3：当前节点是黑色的，兄弟节点是黑色的，且兄弟节点左孩子是红色的，右孩子是黑色的
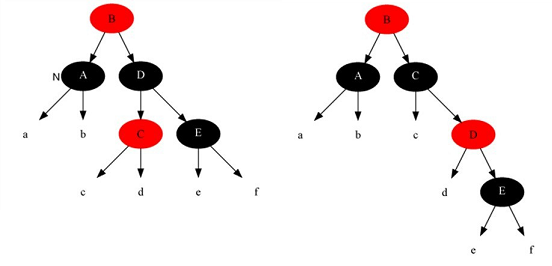
针对这种情况，我们要做的操作有：把当前节点的兄弟节点（D）涂红，把兄弟节点的左子节点（C）涂黑，然后以兄弟节点作为支点做右旋操作。然后兄弟节点就变成黑色的，且兄弟节点的右子节点变成红色的情况（情况4）了。
情况4：当前节点是黑色的，兄弟节点是黑色的，且兄弟节点右孩子是红色的，左孩子的颜色随意
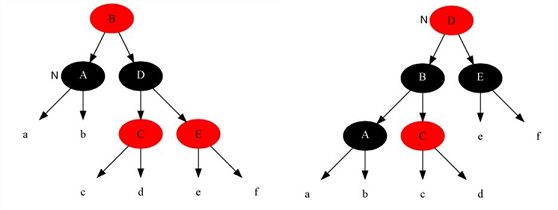针对这种情况，我们要做的操作有：把兄弟节点（D）涂成父节点的颜色，再把父节点（B）涂黑，把兄弟节点的右子节点（E）涂黑，然后以当前节点的父节点为支点做左旋操作。至此，删除修复算法就结束了，最后将根节点涂黑即可。
复杂度分析
从红黑树的插入和删除操作来看，其插入时最多进行两次旋转操作，这与AVL树相同，但是删除时，红黑树最多只需要进行三次旋转操作，而AVL树则可能需要维护整个路径上的节点，所以这一点上，红黑树更占优势，保证了在插入和删除的复杂度都在\(O(\log N)\)的数量级上。
红黑树与2-3-4树
上述的红黑树的解释感觉还是比较抽象，为啥一个AVL树加了两个颜色就变得这样了？
有很多资料也把红黑树看作是一种2-3-4树，这样确实理解起来比直接从红黑树的性质入手更加直观一些，对于红黑树的一些性质也可以有一个更加直接的解释。
简单来说，将一个2-3-4树的3、4节点向下分裂成红节点，就可以得到一棵红黑树。这样也就解释了为什么红黑树不能有两个连续的红色节点，以及为什么红黑树任一节点到叶节点的路径上黑色节点的数量都是一样的。这里就不加以详细解释了，可参考这篇文章
