最短路问题
Dijkstra算法
Dijkstra应该是最经典点的单源最短路算法了,算法的思想是通过不断搜罗已经确定了最短路的顶点,然后更新该点邻接点的最短距离。这里就不多做解释了,下面是dijkstra的伪代码,需要注意的是Dijkstra不能解决有负边的情况。算法复杂度\(O(\|V\|^2 + \|E\|)\), V为顶点数,E为边数。

Floyd-Warshall算法
Floyd-Warshall算法是经典的多源最短路算法,也就是能计算任意两点间的最短距离。它的思路是dp的思想。
在只使用前k个点时,记i,j之间的最短距离为\(d[k][i][j]\),这个最短距离可以有两种情况,一是最短路径不经过点k,那么这时的\(d[k][i][j] = d[k-1][i][j]\),二是最短路径经过点k,那么\(d[k][i][j] = d[k - 1][i][k] + d[k - 1][k][j]\),所以合起来递推公式就是\(d[k][i][j] = min(d[k - 1][i][j], d[k - 1][i][k] + d[k - 1][k][j])\).
Floyd-Warshall算法可以检测负权的存在,只需要检测是否存在\(d[i][j]\)为负的情况就可以了。整体算法复杂度为\(O(\|V\|^3)\)

SPFA算法
SPFA,全称Shortest Path Faster Algorithm,是西南交通大学段凡丁于1994年发表的一个求单源最短路径的算法。从名字就可以知道这个算法相对比较快速。该算法主要用来解决存在负权边的单源最短路径问题,因为Dijkstra不能解决这类问题,而Floyd算法的复杂度又过高。
SPFA算法利用了队列来保存更新过最短距离的节点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对u的邻接点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。 这里的松弛操作其实就是更新最短距离,更新的依据是\(dis[v]>dis[u]+w(u,v)\),如果该式成立则将\(dis[v]\)减小到\(dis[u]+w(u,v)\),否则不动。 这个更新操作是显而易见的,但是这个三角不等式的形式要注意一下,后边会利用到。下边是spfa的一个例子:
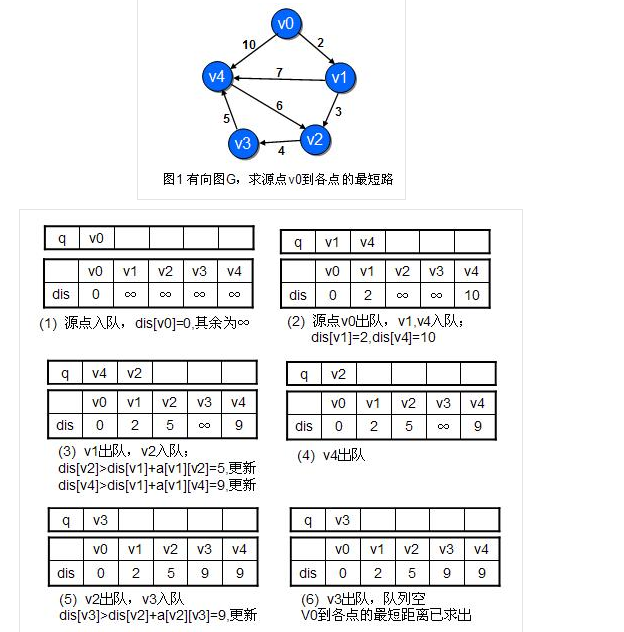
对于存在负圈的情况,如果某个点进入队列的次数超过了顶点的数目,那么就意味着存在负圈。用数组记录每个顶点进入队列的次数,这样就可以检测负圈的存在了。
下面是个伪码(网上抄来的,不一定对)
bool spfa(s) {
for(i = 0; i < n; i++) {
d[i] = (i == s) ? 0 : INF;
inq[i] = (i == s); // 顶点是否在队列中
visitCount[i] = 0; // 进队的次数
}
q.push( (d[s], s) );
while( !q.empty() ) {
(dist, u) = q.front();
q.pop();
inq[u] = false;
if( visitCount[u]++ > n ) { // 判断负圈
return true;
}
for (e = head[u]; e != INF; e = edge[e].next) {
v = edge[e].v;
w = edge[e].w;
if(d[u] + w < d[v]) {
d[v] = d[u] + w;
if ( !inq[v] ) {
nq[v] = true;
q.push( (d[v], v) );
}
}
}
}
return false;
}
最小生成树
对于一个无向图G,如果它的一个包含全部顶点的子图任意两点都连通,而且是一棵树(没有环),那么这棵树就叫做生成树。如果边上有权值,那么使得权值和最小的生成树,叫做最小生成树。最小生成树有几个性质:
- 最小生成树存在,那么图一定连通,反之也成立
- 最小生成树包含V个顶点,那么一定包含V-1条边
要注意的是,生成树和最小生成树都不一定是唯一的。
最小生成树的获取有两种常见的算法,Prim算法和Kruskal算法。两种算法都是采取的贪心的策略,Prim是不断地将一棵小树生长成最终的结果,而Kruskal则是将森林合并成一棵树。
Prim算法
首先,取一个节点作为开始节点,先将其收录到树中,然后找到距离树中节点最近的节点,并将它收录到树中,两者之间的边就是最小生成树中的一条边,更新该节点邻接点中还未收录的节点到树的距离,之后不断重复这个过程。
整个算法和Dijkstra算法很像,不同点在于,Prim关注的是节点到树的距离,而不是到某个开始节点的距离。关于收录节点,只需要另该节点的dist值为0就可以了,而最终结果的存储则是通过保存节点的父节点来实现的。

Kruskal算法
Kruskal算法更加直截了当,选取图中最短的边,并将边的两个端点加入到树的节点中,当然,在收录之前要判断是否成环,这一点可以利用并查集来进行判断——如果一条边的两个顶点不在一个连通分量内,那么加入这一条边就一定不会成环。当然,加入这条边之后,要把两个顶点合并到一个连通分量中。

差分约束系统
如若一个系统由n个变量和m个不等式组成,并且这m个不等式对应的系数矩阵中每一行有且仅有一个1和-1,其它的都为0,这样的系统称为差分约束( difference constraints )系统。例如下图所示的不等式组:
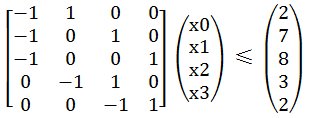
如果要求x[3] - x[0]的最大值,如何计算呢?当然我们可以利用线性规划等优化方法来求,但过于复杂了。
我们来单独观察一个不等式\(x[i] - x[j]\le a[k]\),移一下项,变成\(x[i]\le x[j] + a[k]\),这个形式有没有很眼熟呢?没错,这个和最短路算法中进行松弛的三角不等式是相同的形式,这里的$a[k]$对应着$w(v, u)$,\(x[i]\)和\(x[j]\)分别对应着\(d[u]\)和\(d[v]\)。所以,差分约束系统实际上可以转化成图论中的最短路问题, 对于每个不等式\(x[i] - x[j]\le a[k]\),对结点 \(j\) 和 \(i\) 建立一条 \(j \to i\)的有向边,边权为\(a[k]\),求\(x[n-1] - x[0]\) 的最大值就是求 \(0\) 到\(n-1\)的最短路。
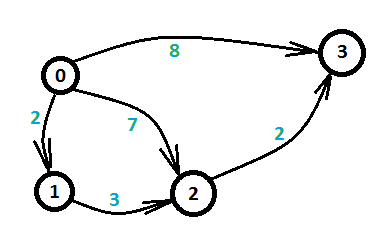
这里看一个简单的例子:
\[\begin{equation}B-A\le c\\C-B\le a\\C-A\le b\end{equation}\]我们想要知道C - A的最大值,通过(1) + (2),可以得到 C - A <= a + c,所以这个问题其实就是求$min(b, a+c)$。将上面的三个不等式按照上面提到的方式建图,可以得到
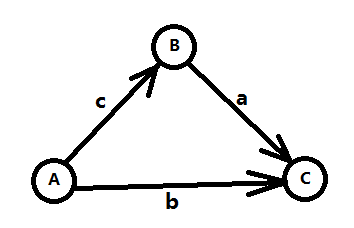
我们发现$min(b, a+c)$正好对应了A到C的最短路。将三个不等式推广到m个,变量推广到n个,就变成了n个点m条边的最短路问题了。
解的存在性
在求最短路的时候,会出现负圈或者根本两点之间不可达的情况。对于负圈,说明两点之间的最短路无限小,对应到不等式中,就是\(x[i] - x[j] < =T\)中的T无限小,所以\(x[i] - x[j]\)的最大值不存在。
而对于不可达的情况,说明两者之间的最短距离无限大,对应到不等式,也就是所求的最大值也无限大。
不等式的标准化
对于有些题目,所求的是最小值,而不是最大值这时只要把不等式中的\(\le\)变成\(\ge\),求最短路变成求最大路就可以了。
如果给出的约束不等式既有\(\le\)又有\(\ge\),那么要根据最后求的是最大值还是最小值进行不等式的转化,而如果约束中有\(A-B = c\)这样的等式的话,那么就把它转化为两个不等式,\(A - B\le c\) 和\(A-B\ge c\),然后根据需要将一个不等式反号就可以了。
最后,如果这些变量都是整数域上的,那么遇到A - B < c这样的不带等号的不等式,我们需要将它转化成”<=”或者”>=”的形式,即 A - B <= c - 1。
最后这个没有太懂,没看到具体例子
参考资料
-
《挑战程序设计竞赛》